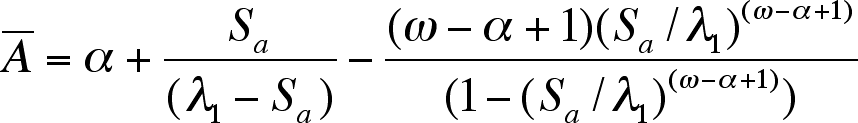1. An Example using the Barndoor Skate
The vital rates of elasmobranchs and other long-lived marine species are not well known and population growth rates are mere guesstimates. However, elasticities are fairly robust even if the population growth rates are not very precise and do allow formulation of management proposal. My analysis indicates that the elasticity pattern can be predicted with a minimal amount of calculations and that it is determined by age-at-first reproduction (α, alpha) and the mean age of reproducing females (Ā, Abar) at the stable age-distribution. Knowledge of the gestation period (GP) may allow a refinement but here I assume GP = 0 in the formulas given in Mollet and Cailliet (2003, Appendix1b, normalized elasticities; i.e. sum is now 1.0 whereas before normalization the sum of the elasticities is 1+ E1):
E(fertility) = E1 = 1/(Ā + 1);
E(juvenile survival) = E2 = (α)/(Ā + 1);
E(adult survival) = E3 = (Ā - α)/(Ā + 1).
All we need to calculate the E-pattern of an elasmobranch is alpha and Abar. Easier said than done because the exact formula given below for Abar requires lambda. However, we can proceed with several approximations and compare them with the "correct" E-pattern. The barndoor skates shall serve as an example. The complete Leslie matrix with solution and the calculation of the E-pattern are included in the table below with a link already provided here. The "correct" normalized E-pattern is E1 = 0.08751, E2 = 0.7876, E3 = 0.1249. (E2/E1 = 9.0, E3/E1 = 1.43; E2/E1 + E3/E1 = 10.43 = Abar) . [Note that E2 >> E3 (E2/E3 = 6.3) as pointed out by Mollet and Cailliet (2003) when discussing Frick MG, Miller TJ, & Fogerty MJ (2002) who reported that E3 > E2. Accordingly, they were "off" by at least a factor of 6.3, almost an order of magnitude.
Abar can be calculated from the following 3-term formula which assumes constant fertility (m) and adult survival (Sa):
while perhaps intimating at first, it is just a formula that is easily calculated.
1st Approximation. Abar (mean age of reproducing female) must be at least alpha (age at first reproduction), I will use Abar = 9.1 instead of 9.0 to avoid E3 = 0.0.
Using this value for the barndoor skate we obtain the following approximate E-pattern: E1 = 1/10.1 = 0.099; E2 = 9/10.1 = 0.891; E3 = 0.1/10.1 = 0.01. Note that this calculation predicts that E3 (elasticity of adult survival) is negligibly small. While certainly a rough approximation, it actually provides a much better approximation for the purpose of a management proposal than what was reported by Frick MG, Miller TJ, & Fogerty MJ (2002) who claimed that the elasticity of adult survival (E3) was larger than the elasticity of juvenile survival (E2).
2nd Approximation based on two terms in the above formula [Abar = alpha + Sa/(lambda-Sa)] with Sa =0.73564 and assuming lambda = 1.0 (stationary age distribution): Abar = 9.000 + 0.73564/(1.0 - 0.73564) = 11.783 which produces the following E-pattern: E1 = 1/12.783 = 0.078, E2 = 0.704, E3 = 0.218 which yields E2/E3 = 3.23.
3rd Approximation based on two terms in above formula but now using calculated lambda = 1.1624: Abar = 9.0000 + 0.7356/(1.1624 - 0.7356) = 10.7238 which produces the following E-pattern: E1 = 0.0883, E2 = 0.7677, E3 = 0.1470 which yields E2/E3 = 5.22.
4th "Approximation'" using all three terms in formula above gives Abar = 9.0000 + 1.7238 - 0.2967 = 10.4271 and the following E-pattern E1 = 0.08751, E2 = 0.7876, E3 = 0.1249 which yields E2/E3 = 6.31. "Approximation" in the sense that the parameters used are estimates. Using all 3 terms in the formula for Abar provides of course an exact result.
Note that Frick MG, Miller TJ, & Fogerty MJ (2002) used somewhat different vital rates (alpha = 15 yr, omega = 50 yr, S1 = 0.30000, S2-S50 = 0.91393 which produces a somewhat different E-pattern which would yield E2/E3 = 3.98 if the E-pattern is correctly calculated. They had used a stage-based model for the barndoor skate and incorrectly found that E3 > E2 which would lead to wrong management proposals.
The above formulas for the E-pattern can be used to calculate the requirement that E3 becomes at least as large as E2 which is Abar = 2 * alpha. If alpha used is 15 yr, then Abar would have to be at least 30 yr. This would require much larger survival rates, survival rates that would be more appropriate for a mammal than an elasmobranch.
2. A Table with Demographic Results for many Elasmobranchs
There is no need to fill in the gaps in this table because the E-pattern for all sharks has E3/E2 < 1 because Abar/alpha < 2 (see table below). In cases where the original calculations were carried out with a stage-based model, I have indicated that the calculated E-pattern is not correct unless it is calculated empirically.
Section 4. below refers to a pdf with calculated and graphed E-patterns for 66 shark populations which included the sharks listed in the table below. The calculation of Abar requires lambda (see above) and thus the Euler equation has to be solved. At a more basic level it can be shown that sharks with omega/alpha <= 3 must have Abar/alpha < 2 and for the sharks with omega/alpha > 3, x = Sa/lambda is sufficiently smaller than 1.0 such that E3/E2 is still <1.0 .
[Alpha = age-at-first-reproduction, Abar = mean age of reproducing females. at the stable age distribution, omega = maximum age (longevity estimate)]
|
Elasmobranch |
Vital Rates or Preliminary Demography |
Elasticity Pattern & Determining Parameters |
Demography Publications |
||||
|---|---|---|---|---|---|---|---|
| E1 (%) | E2 (%) |
E3 (%) |
Abar/alpha | Omega/alpha | |||
|
Angel shark, Squatina californica Ayres, 1859 |
~E-pattern based on Mu1 =14.5 yr given in Cailliet et al. 1992 | ~6.4 |
~64.5 |
~29.0 |
~1.5 |
3.5 |
Cailliet et al. 1992, (download pdf); Heppell et al. 1999; Smith et al. 1999; Cortes 2002; |
Barndoor skate,
Dipturus laevis Mitchill, 1817
|
8.75 |
78.8 |
12.5 |
1.159 |
1.667 |
Frisk et al (2002) but see Mollet and Cailliet (2003) for errors made because stage-based model was used. |
|
|
Basking shark,
Cetorhinus maximus (Gunnerus, 1765)
|
3.94
|
71.0 |
25.1 |
1.353 |
2.222 |
||
Bat ray, Myliobatis californica (Gil~l 1865) |
~10.0 |
~60.0 |
~30.0 |
assumed 1.50 |
|||
|
Blue shark, Prionace glauca (Linnaeus, 1758) |
|||||||
|
Bull shark |
|||||||
|
Catshark, brown, Apristurus brunneus (Gilbert, 1892) |
|||||||
|
Catshark, filetail, Parmaturus xaniuru (Gilbert, 1892) |
|||||||
|
Dogfish, spiny, Squalus acanthia (Linnaeus, 1758) |
|||||||
|
Leopard shark, Triakis semifasciata Girard, 1854 |
5.74
|
68.9 |
25.3 |
1.368 |
check |
||
|
Horn shark, Heterodontus francisci (Girard, 1854) |
|||||||
|
Mako, shorfin , Isurus oxyrinchus Rafinesque, 1809 |
9.34 |
65.4 |
25.3 |
1.387 |
3.0 |
||
|
Mako, longfin , Isurus paucus Guitard, 1966 |
|||||||
|
Oceanic whitetip shark, Carcharhinus longimanus (Poey, 1861) |
|||||||
|
Pacific sleeper shark, Somniosus pacificus Bigelow and Schroeder, 1944 |
|||||||
|
Pelagic stingray, Dasyatis (Pteroplatytrygon) violacea (Bonaparte, 1832) |
19.6 |
58.8 |
21.7 |
1.368 |
3.333 |
||
|
(Porbeagle, NWA, Lamna nasus (Bonnaterre, 1788)) |
5.58
|
75.1 |
19.1 |
1.255 |
2.308 |
Cortes 2002;
Campana et al. (in press) |
|
|
Prickly shark, Echinorhinus cookei Pietschmann, 1928 |
|||||||
|
(Sandbar shark, NWA) |
|||||||
|
Salmon shark, Lamna ditropis Hubbs & Follett, 1947 |
7.50 |
67.5 |
25.0 |
1.371 |
check |
||
|
Sandtiger Shark, NWA,
Carcharias taurus
(Rafinesque, 1810) |
9.17 |
55.0 |
35.8 |
1.650 |
4.167 |
||
|
School shark, Galeorhinus galeus |
|||||||
|
Sevengill shark, Notorynchus cepedianus (Peron, 1807) |
4.97 |
79.4 |
15.6 |
1.196 |
2.813 |
Smith et al. 1999; |
|
|
Sixgill shark, Hexanchus griseus (Bonnaterre, 1788) |
|||||||
|
Smoothhound, brown
Mustelus henlei (Gill, 1863)
|
17.6 |
52.8 |
29.6 |
1.560 |
3.000 check |
||
|
Smoothhound, gray Mustelus californicus Gill, 1864 |
17.2
|
51.7 |
31.0 |
1.600 |
4.333 check |
||
|
Soupfin shark Mustelus californicus Gill, 1864 |
|||||||
|
Swell shark
Cephaloscyllium ventriosum (Garman, 1880)
|
|||||||
|
Thresher shark, bigeye Alopius supersiliosus (Lowe, 1839) |
|||||||
|
Thresher shark, common Alopius vulpinus (Bonnaterre, 1788) |
|||||||
|
Thresher shark, pelagic Alopius pelagicus Nakamura, 1935 |
|||||||
|
Tiger shark Galeocerdo cuvier (Peron & LeSueur, 1822) |
|||||||
|
Whale Shark
Rhincodon typusSmith, 1828
|
4.29 |
77.3 |
18.5 |
1.239 |
3.055 |
Bradshaw, Mollet, Meekan (2007) Tables 3 &4 have E-patterns for 4 scenarios using 1-yr & 2-yr projection interval |
|
|
White Shark Carcharodon carchariasÊ (Linnaeus, 1758) |
|||||||
| Elasmobranch |
Vital Rates or Preliminary Demography |
Elasticity Pattern & Determining Parameters |
Publications |
||||
| E1 (%) | E2 (%) |
E3 (%) |
Abar/alpha | Omega/alpha | |||